Tema. Cómo obtener una regla o fórmula para una sucesión numérica.
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
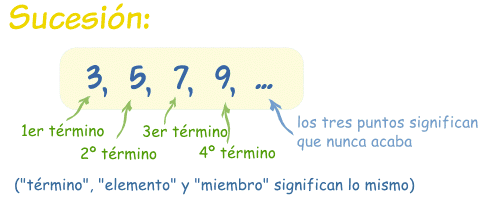 |
La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
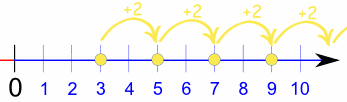
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|---|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|---|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
Posición del término | |
 |
Es normal usar xn para los términos:
|
| Así que para hablar del "quinto término" sólo tienes que escribir: x5 |
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Actividad. Utiliza las siguientes reglas para calcular las posiciones 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10.
1n+3
2n-6
2n+7
11n+5
16n+9
12n-4
-8n+3
-6n+6
-7n+10
-5n+4
-4n-10
-8n-14