Actividad. Resuelve las siguientes ecuaciones obteniendo el valor desconocido y realiza la comprobación.
5x-15=15
2x-13=-19
7x+5=-100
-12x-15=9
5x-14=-74
8x-5=-109
-13x-6=-97
martes, 31 de enero de 2017
B3. Act. 26. Ecuaciones. 2/2/17
B3. Act. 26. Ecuaciones. 2/2/17
Actividad. Resuelve las siguientes ecuaciones obteniendo el valor desconocido y realiza la comprobación.
8x-5=-109
2x+6=-12
-13x-6=-97
Actividad. Resuelve las siguientes ecuaciones obteniendo el valor desconocido y realiza la comprobación.
8x-5=-109
-13x-6=-97
B3. Act. 25. Ecuaciones. 1/2/17
B3. Act. 25. Ecuaciones. 1/2/17
Tema. Ecuaciones de primer grado. Forma ax+b=c
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
c representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
1. los términos que tienen x se anotan del lado izquierdo del signo igual, considerando qué cambia que el término que se mueve cambia a su operación contraria.
2. los términos que no tienen x se anotan de lado derecho del signo igual, considerando qué el término que se mueve cambia a su operación contraria.
3. se resuelven las operaciones correspondientes cuidando los signos
4. el número que acompaña a la letra x, se mueve al otro lado para hacer la división.
5. el resultado se utiliza para hacer la comprobación.
Ejemplo.
Ejemplo.
Actividad: Resuelve las siguientes ecuaciones, respeta las indicaciones.
Tema. Ecuaciones de primer grado. Forma ax+b=c
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
c representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
1. los términos que tienen x se anotan del lado izquierdo del signo igual, considerando qué cambia que el término que se mueve cambia a su operación contraria.
2. los términos que no tienen x se anotan de lado derecho del signo igual, considerando qué el término que se mueve cambia a su operación contraria.
3. se resuelven las operaciones correspondientes cuidando los signos
4. el número que acompaña a la letra x, se mueve al otro lado para hacer la división.
5. el resultado se utiliza para hacer la comprobación.
Ejemplo.
-11x+12
|
=
| 144 |
-11x
|
=
| 144-12 |
-11x
|
=
| 132 |
x
|
=
| 132/-11 |
x
|
=
| -12 |
Comprobación
|
-11(-12)+12
|
=
| 144 |
132+12
|
=
| 144 |
144
|
=
| 144 |
Ejemplo.
-8x-15
|
=
| -111 |
-8x
|
=
| -111+15 |
-8x
|
=
| -96 |
x
|
=
| -96/-8 |
x
|
=
| 12 |
Comprobación
|
-8(12)-15
|
=
| -111 |
-96-15
|
=
| -111 |
-111
|
=
| -111 |
Actividad: Resuelve las siguientes ecuaciones, respeta las indicaciones.
6x-10=-16
-15x-6=9
12x+12=72
-10x+9=-81
B3. Act. 24. Ecuaciones. 1/2/17
B3. Act. 24. Ecuaciones. 1/2/17
Tema. Ecuaciones en la forma ax=b
Los pasos para resolver este tipo de ecuación son:
1. Se acomodan los términos, del lado izquierdo el signo igual está la letra x, del lado derecho del signo igual se anota el número que acompañaba a la letra x y será el divisor.
2. Se resuelve la división correspondiente cuidando que el resultado tenga el signo correcto.
3. El valor desconocido será el resultado de la división y se usará para hacer la comprobación.
Ejemplo.
6x=48 ecuación original
x= 48÷6 se acomodan los números
x= 8 este es el resultado y se usará para la comprobación
COMPROBACIÓN.
6(8)=48 el valor desconocido se anota en el lugar de la letra x y se usará para multiplicarlo.
48=48 el resultado es correcto
Actividad. Resuelve las siguientes ecuaciones anotando cada paso para saber el valor desconocido y su comprobación.
7x=490
12x=-144
-7x=35
-17x=-68
3x=69
Tema. Ecuaciones en la forma ax=b
Los pasos para resolver este tipo de ecuación son:
1. Se acomodan los términos, del lado izquierdo el signo igual está la letra x, del lado derecho del signo igual se anota el número que acompañaba a la letra x y será el divisor.
2. Se resuelve la división correspondiente cuidando que el resultado tenga el signo correcto.
3. El valor desconocido será el resultado de la división y se usará para hacer la comprobación.
Ejemplo.
6x=48 ecuación original
x= 48÷6 se acomodan los números
x= 8 este es el resultado y se usará para la comprobación
COMPROBACIÓN.
6(8)=48 el valor desconocido se anota en el lugar de la letra x y se usará para multiplicarlo.
48=48 el resultado es correcto
Actividad. Resuelve las siguientes ecuaciones anotando cada paso para saber el valor desconocido y su comprobación.
7x=490
12x=-144
-7x=35
-17x=-68
3x=69
B3. Act. 23. Ecuaciones. 31/1/17
B3. Act. 23. Ecuaciones. 31/1/17
Tema. Ecuaciones de primer grado. Forma x+a=b
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
x+24=55
pasó 1 Se acomodan los términos, del lado izquierdo del signo igual se anota la x, del lado derecho del signo igual se anotan los números. Considerando que el número qué cambia de posición también cambiará de signó.
x=55-24 sólo cambió el 24 positivo a negativo, el 55 no cambia de signo porque no lo movimos
pasó 2 se resuelve la operación
x=31
pasó 3 el resultado se utiliza para realizar la comprobación
31+24=55 el resultado que en este caso es 31 se nota en lugar de la letra x, ahora se resuelve la operación y se comprueba qué 31 es el valor correcto.
Actividad. Resuelve las siguientes ecuaciones de acuerdo al proceso indicado previamente.
Tema. Ecuaciones de primer grado. Forma x+a=b
Una ecuación es una operación en la que debemos calcular el valor de un número desconocido.
Debemos considerar lo siguiente:
x es el valor desconocido
a representa un número
b representa un número
Los pasos para resolver una ecuación de esta forma son:
ECUACIÓN ORIGINAL.
x+24=55
pasó 1 Se acomodan los términos, del lado izquierdo del signo igual se anota la x, del lado derecho del signo igual se anotan los números. Considerando que el número qué cambia de posición también cambiará de signó.
x=55-24 sólo cambió el 24 positivo a negativo, el 55 no cambia de signo porque no lo movimos
pasó 2 se resuelve la operación
x=31
pasó 3 el resultado se utiliza para realizar la comprobación
31+24=55 el resultado que en este caso es 31 se nota en lugar de la letra x, ahora se resuelve la operación y se comprueba qué 31 es el valor correcto.
Actividad. Resuelve las siguientes ecuaciones de acuerdo al proceso indicado previamente.
lunes, 30 de enero de 2017
B3. Act. 22. Sucesión numérica. 30/1/17
B3. Act. 22. Sucesión numérica. 30/1/17
Actividad. Calcula las siguientes posiciones 1 a 5 para cada regla de sucesión numérica.
12n-8
16n-15
14n-10
-9n+3
-7n+6
-8n+10
-5n+4
-6n-10
Actividad. Calcula las siguientes posiciones 1 a 5 para cada regla de sucesión numérica.
12n-8
16n-15
14n-10
-9n+3
-7n+6
-8n+10
-5n+4
-6n-10
miércoles, 25 de enero de 2017
B3. Act. 21. Sucesiones numéricas. 26/1/17
B3. Act. 21. Sucesiones numéricas. 26/1/17
Actividad. Encuentra las posiciones para cada una de las reglas.
Posiciones. 4, 8, 12, 14, 16, 20, 24, 28, 32, 36
15n-15
10n-34
25n+69
3n-1
-1n-1
-5n+5
-6n-3
-2n+5
5n-2
2n+3
10n-5
4n+8
1n+2
4n+1
25n+1
Actividad. Encuentra las posiciones para cada una de las reglas.
Posiciones. 4, 8, 12, 14, 16, 20, 24, 28, 32, 36
15n-15
10n-34
25n+69
3n-1
-1n-1
-5n+5
-6n-3
-2n+5
5n-2
2n+3
10n-5
4n+8
1n+2
4n+1
25n+1
B3. Act. 20. Sucesiones numéricas. 25/1/17
B3. Act. 20. Sucesiones numéricas. 25/1/17
Actividad. Calcula las siguientes posiciones para cada regla de sucesión numérica. 3,5,8,9,12,21,25,26,31,37
-5n+7
-12n-9
-15n+11
-22n+15
1.5n-2.4
Actividad. Calcula las siguientes posiciones para cada regla de sucesión numérica. 3,5,8,9,12,21,25,26,31,37
-5n+7
-12n-9
-15n+11
-22n+15
1.5n-2.4
martes, 24 de enero de 2017
B3. Act. 19. Sucesión numérica. 24/1/17
B3. Act. 19. Sucesión numérica. 24/1/17
Tema. Cómo obtener una regla o fórmula para una sucesión numérica.
Actividad. Utiliza las siguientes reglas para calcular las posiciones 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10.
1n+3
2n-6
2n+7
11n+5
16n+9
12n-4
-8n+3
-6n+6
-7n+10
-5n+4
-4n-10
-8n-14
Tema. Cómo obtener una regla o fórmula para una sucesión numérica.
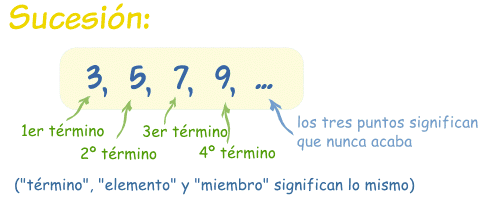
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
 |
La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
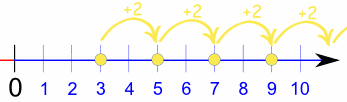
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|---|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|---|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
Posición del término | |
 |
Es normal usar xn para los términos:
|
| Así que para hablar del "quinto término" sólo tienes que escribir: x5 |
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Actividad. Utiliza las siguientes reglas para calcular las posiciones 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10.
1n+3
2n-6
2n+7
11n+5
16n+9
12n-4
-8n+3
-6n+6
-7n+10
-5n+4
-4n-10
-8n-14
B3. Act. 18. Examen. 23/1/17
B3. Act. 18. Examen. 23/1/17
Actividad. Examen pegado y firmado por el padre o tutor.
Actividad. Examen pegado y firmado por el padre o tutor.
domingo, 15 de enero de 2017
B3. Act. 17. Media ponderada. 19/1/17
B3. Act. 17. Media ponderada. 19/1/17
Actividad. Obtén la media ponderada de cada grupo de datos.
8(4), 2(6), 5(3), 2(9), 1(5)
3(1), 6(7), 2(4), 3(6), 1(1), 3(3)
5(8), 8(2), 8(5), 2(8), 4(2)
10(10), 9(6), 5(4), 8(8), 4(2), 10(5)
9(3), 8(7), 4(2), 10(3), 7(5), 2(4)
5(2), 4(8), 10(4), 4(7), 2(8), 4(1)
Actividad. Obtén la media ponderada de cada grupo de datos.
8(4), 2(6), 5(3), 2(9), 1(5)
3(1), 6(7), 2(4), 3(6), 1(1), 3(3)
5(8), 8(2), 8(5), 2(8), 4(2)
10(10), 9(6), 5(4), 8(8), 4(2), 10(5)
9(3), 8(7), 4(2), 10(3), 7(5), 2(4)
5(2), 4(8), 10(4), 4(7), 2(8), 4(1)
B3. Act. 16. Media ponderada. 18/1/17
B3. Act. 16. Media ponderada. 18/1/17
Tema. Media ponderada.
La media ponderada se obtiene al otorgar un valor a cada uno de los datos de un grupo de datos.
Para ello se multiplica cada dato por el valor asignado y se dividirá entre la suma de todos los valores. El resultado será la media ponderada.
La calificación final de una asignatura es un ejemplo de una media ponderada ya que cada una de las variables tiene un valor.
En el siguiente ejemplo el examen inicial tiene un valor de 3, el trabajo escrito 1, el trabajo final 2 y el examen final 4.
Tema. Media ponderada.
La media ponderada se obtiene al otorgar un valor a cada uno de los datos de un grupo de datos.
Para ello se multiplica cada dato por el valor asignado y se dividirá entre la suma de todos los valores. El resultado será la media ponderada.
La calificación final de una asignatura es un ejemplo de una media ponderada ya que cada una de las variables tiene un valor.
En el siguiente ejemplo el examen inicial tiene un valor de 3, el trabajo escrito 1, el trabajo final 2 y el examen final 4.
Se multiplica la calificación de cada una de las variables por el valor qué se le asignó, todos estos resultados se suman y se dividen entre la cantidad de valores que se otorgaron.
La nota final del alumno en esta asignatura es de 6,14. como la nota es muy próxima a las notas sacadas en los exámenes. Esto es a causa de que los exámenes eran más importantes y tenían unos pesos mucho mayores que los de los trabajos.
Actividad. Calcula la media ponderada de cada uno de los grupos datos.
Nota. El número sin paréntesis es el dato y el número a un lado dentro del paréntesis es el valor.
3(1),4(3),6(9),2(2),5(4)
5(2),3(3),9(9),3(4),5(6)
3(2),6(9),9(4),12(11),15(20)
1(2),3(4),5(6),8(7),9(10)
2(1),3(2),1(4),5(2),2(5)
9(1),8(5),3(2),2(1),6(3)
B3. Act. 15. Análisis de datos. 17/1/17
B3. Act. 15. Análisis de datos. 17/1/17
Actividad. Obtén la moda, media y mediana de los siguientes grupos de datos.
3, 9, 11, 6, 12, 14, 8, 2, 9
12, 4, 23, 6, 9, 13, 8, 16, 21, 4
23, 6, 9, 6, 12, 14, 5, 9, 10, 21
15, 4, 8, 10, 5, 15, 12, 16, 21, 24
16, 21, 24, 34, 56, 75, 56, 43, 32, 23
Actividad. Obtén la moda, media y mediana de los siguientes grupos de datos.
3, 9, 11, 6, 12, 14, 8, 2, 9
12, 4, 23, 6, 9, 13, 8, 16, 21, 4
23, 6, 9, 6, 12, 14, 5, 9, 10, 21
15, 4, 8, 10, 5, 15, 12, 16, 21, 24
16, 21, 24, 34, 56, 75, 56, 43, 32, 23
B3. Act. 14. Análisis de datos. 16/1/17
B3. Act. 14. Análisis de datos. 16/1/17
Tema. Análisis de datos.
En un grupo de datos se pueden analizar los siguientes elementos:
1. Moda: la moda se refiere a los datos que aparecen con mayor frecuencia, si hay 2 modas se llama bimodal, si hay más de dos será multimodal.
2, 3, 3, 4, 4, 4, 5, 5
Moda= 4.
2. Mediana: es el número que se encuentra a la mitad de un grupo de datos, después de que han sido ordenados de menor a mayor o viceversa.
2, 3, 4, 4, 5, 5, 5, 6, 6.
Mediana=5
Si la cantidad de datos es par la mediana será el promedio de las dos cantidades.
7, 8, 9, 10, 11, 12
9+10=19. 19÷2=9.5
Mediana= 9.5
3. Media o promedio: es el número obtenido a partir de la suma de todos los datos, dividida entre la cantidad de datos.
14, 54, 25, 32, 47, 28
Suma 200÷6=33.3
Media o promedio = 33.3
Actividad. analiza la siguiente situación y obtén la moda, la media y la mediana.
8, 10, 9, 1, 6, 9,
15, 8, 12, 2, 1, 13, 2
2, 10, 9,12, 4, 3, 8, 15
17, 6, 8, 9, 5, 9, 10, 5, 15
23, 6, 9, 6, 12, 14, 5, 9, 10, 21
15, 4, 8, 10, 5, 15, 12, 16, 21, 24
Tema. Análisis de datos.
En un grupo de datos se pueden analizar los siguientes elementos:
1. Moda: la moda se refiere a los datos que aparecen con mayor frecuencia, si hay 2 modas se llama bimodal, si hay más de dos será multimodal.
2, 3, 3, 4, 4, 4, 5, 5
Moda= 4.
2. Mediana: es el número que se encuentra a la mitad de un grupo de datos, después de que han sido ordenados de menor a mayor o viceversa.
2, 3, 4, 4, 5, 5, 5, 6, 6.
Mediana=5
Si la cantidad de datos es par la mediana será el promedio de las dos cantidades.
7, 8, 9, 10, 11, 12
9+10=19. 19÷2=9.5
Mediana= 9.5
3. Media o promedio: es el número obtenido a partir de la suma de todos los datos, dividida entre la cantidad de datos.
14, 54, 25, 32, 47, 28
Suma 200÷6=33.3
Media o promedio = 33.3
Actividad. analiza la siguiente situación y obtén la moda, la media y la mediana.
8, 10, 9, 1, 6, 9,
15, 8, 12, 2, 1, 13, 2
2, 10, 9,12, 4, 3, 8, 15
17, 6, 8, 9, 5, 9, 10, 5, 15
23, 6, 9, 6, 12, 14, 5, 9, 10, 21
15, 4, 8, 10, 5, 15, 12, 16, 21, 24
Suscribirse a:
Entradas (Atom)